快速排序

思路

如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间，中间位置计为 q。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间 q 是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

然后根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

为了便于理解，以数组 [6, 11, 3, 9, 8] 为例，我画了如下图

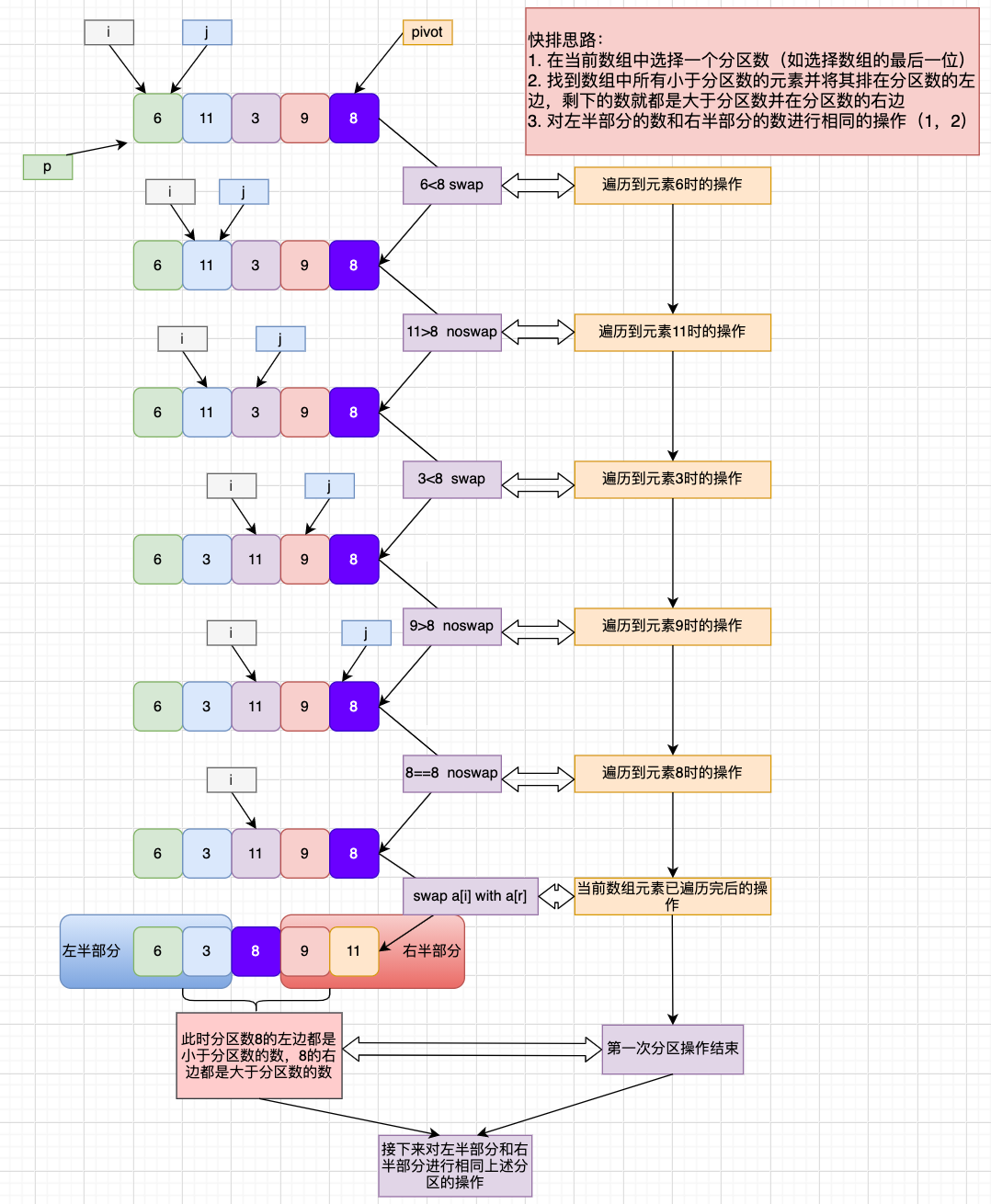
代码

// 交换数组中指定位置的值
function swap(arr, i, j) {
  let temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}

/**
 * 在数组中选择一个数作为分区元素，将所有小于该分区元素的数排在它的左边，
 * 所有大于该分区元素的数排在它的右边，并返回该分区元素所在的位置（索引）
 * @param {*} arr 数组
 * @param {*} start 数组下标起始位置
 * @param {*} end 数组下标结束位置
 * @returns 
 */
function partition(arr, p, r) {
  let pivot = arr[r]; //选择数组的最后一个元素作为分区数
  let i = p;
  for (let j = p; j <= r; j++) {// 遍历该数组区间（p到r区间）的所有元素
    if (arr[j] < pivot) {
      swap(arr, i++, j)
    }
  }
  // 数组遍历完成后，i所指向的位置即为分区数所应在的位置
  // 所以将位置i的元素和区间最后一个元素进行交换
  swap(arr, i, r);
  return i;
}

/**
 * 快速排序
 * @param {*} arr 数组
 * @param {*} n 数组空间大小
 */
function quickSort(arr, n) {
  function _quickSort(arr, p, r) {
    if (p >= r) return;
    const q = partition(arr, p, r);
    // 此时区间 [p, q-1] 的元素都小于索引为q的元素， [q + 1, r] 的元素都大于索引为q的元素，
    _quickSort(arr, p, q - 1)
    _quickSort(arr, q + 1, r);
  }
  _quickSort(arr, 0, n - 1);
}


const arr = [11, 8, 3, 9, 7, 1, 2, 5];
quickSort(arr, arr.length)
console.log(arr)

复杂度分析

假设数组的空间大小为n，针对于快排的时间复杂度分析，我分成了两种情况

1. 最好情况时间复杂度

   假设每一次分区操作可以正好将区间中的数分成大小相同的两部分（左半部分、右半部分），其中左半部分和右半部分的元素个数相同。那么时间复杂度 $T(n)=n+2T(\frac{n}{2})$。其中 $n$ 表示每次分区都需要遍历 $n$(该区间元素个数) 个元素，所需时间复杂度为 $O(n)$。通过时间复杂度公式 $T(n)=n+2T(\frac{n}{2})$，可以推导出 $O(n\log n)$，具体的推到过程如下:

   由于

   $$T(n)=n+2T(\frac{n}{2})$$

   所以

   $$T(\frac{n}{2})=\frac{n}{2}+2T(\frac{n}{4})$$

   所以

   $$T(\frac{n}{4})=\frac{n}{4}+2T(\frac{n}{8})$$

   由上式可知

   $$T(n)=n+2[\frac{n}{2}+2T(\frac{n}{4})]=2n+4T(\frac{n}{4})=2n+4[\frac{n}{4}+2T(\frac{n}{8})]=3n+8T(\frac{n}{8})$$

   即

   $$T(n)=3n+8T(\frac{n}{8})$$

   以此类推，当进行到第 $q$ 次分区时

   $$T(n)=qn+2^qT(\frac{n}{2^q})$$

   当 $T(\frac{n}{2^q})=T(1)$ ，即当数据规模为 $1$ 时，也就是数组中只有一个元素时停止分区操作，即完成快速排序。此时 $\frac{n}{2^q}=1$，即 $q=\log_2n$。于是将 $q=\log_2n$ 代入上式可得

   $$T(n)=n\log_2n+nT(1)\sim n\log_2n$$

   即最好情况下的时间复杂度为 $n\log_2n\sim n\log n$，即为 $O(n\log n)$

2. 平均时间复杂度

   快速排序在最好情况下，每次分区都能一分为二，这个时候用递推公式 $T(n)=n+2T(\frac{n}{2})$，很容易就能推导出时间复杂度是 $O(n\log n)$。但是，我们在实际开发过程中并不可能每次分区都这么幸运，正好一分为二。

   我们假设平均情况下，每次分区之后，两个分区的大小比例为 $1:k$。当 $k=9$ 时，如果用递推公式的方法来求解时间复杂度的话，递推公式就写成 $T(n)=T(\frac{n}{10}​)+T(\frac{9n}{10}​)+n$。这个公式可以推导出时间复杂度，但是推导过程非常复杂。那我们来看看，用递归树来分析快速排序的平均情况时间复杂度，是不是比较简单呢？

   我们还是取 $k$ 等于 $9$，也就是说，每次分区都很不平均，一个分区是另一个分区的 $9$ 倍。如果我们把递归分解的过程画成递归树，就是下面这个样子：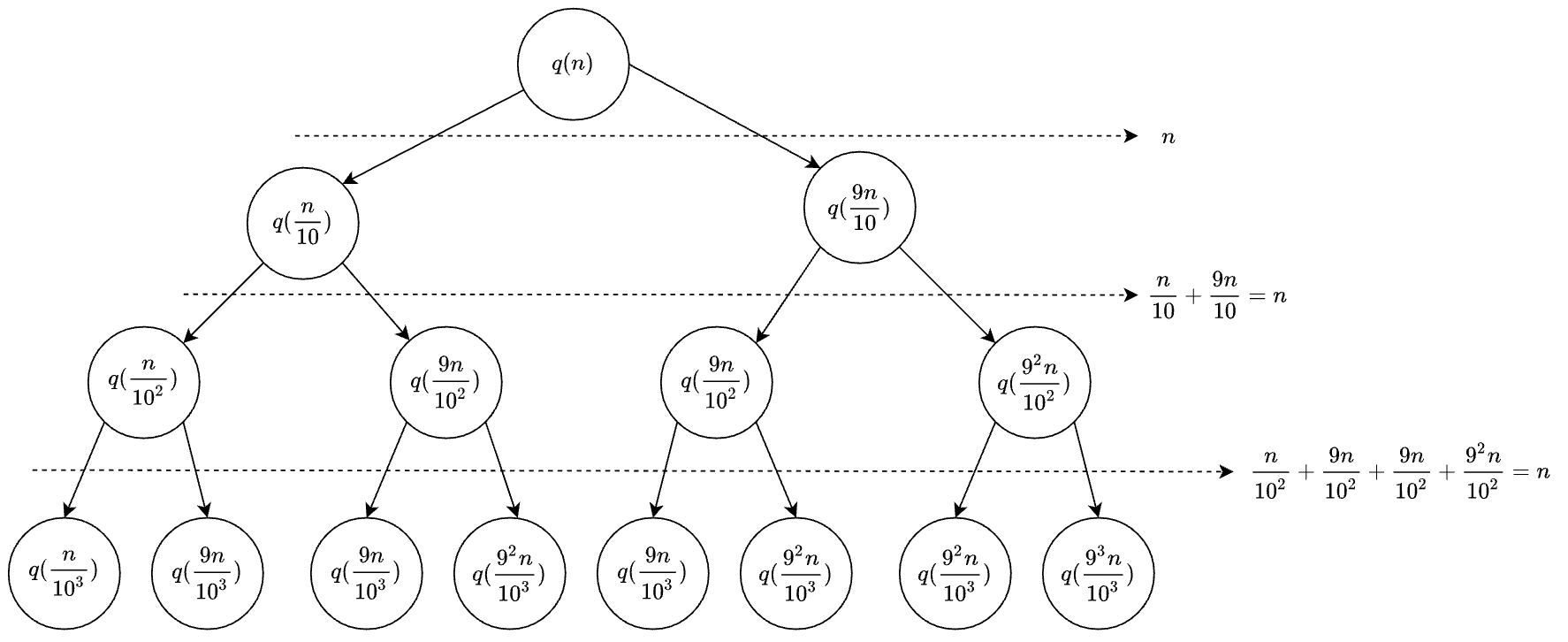

   

   快速排序的过程中，每次分区都要遍历待分区区间的所有数据，所以，每一层分区操作所遍历的数据的个数之和就是 $n$。我们现在只要求出递归树的高度 $h$，这个快排过程遍历的数据个数就是 $h∗n$ ，也就是说，时间复杂度就是 $O(h∗n)$。

   因为每次分区并不是均匀地一分为二，所以递归树并不是满二叉树。这样一个递归树的高度是多少呢？

   我们知道，快速排序结束的条件就是待排序的小区间，大小为$1$，也就是说叶子节点里的数据规模是$1$。从根节点 $n$ 到叶子节点 $1$，递归树中最短的一个路径每次都乘以 $\frac{1}{10}$​，最长的一个路径每次都乘以 $\frac{9}{10}$。通过计算，我们可以得到，从根节点到叶子节点的最短路径是 $\log_{10} ​n$，最长的路径是 $\log_{\frac{10}{9}} n$。具体推到过程如下：

   • 假设树的最小高度为 $h1$（最短路径），那么对应的树的叶子节点（数据规模为$1$）的值应该等于 $n*(\frac{1}{10})^{h1}$，即 $n*(\frac{1}{10})^{h1}=1$，所以 $n=10^{h1}$，所以 $h1=\log_{10} ​n$

   • 同理，假设树的最大高度为 $h2$（最长路径），那么对应的树的叶子节点（数据规模为$1$）的值应该等于 $n*(\frac{9}{10})^{h2}$，即 $n*(\frac{9}{10})^{h2}=1$，所以 $n=(\frac{10}{9})^{h2}$，所以 $h2=\log_{\frac{10}{9}} ​n$

   所以，遍历数据的个数总和就介于 $n\log_{10} ​n$ 和 $n\log_{\frac{10}{9}}​​n$ 之间。根据复杂度的大 $O$ 表示法，对数复杂度的底数不管是多少，我们统一写成 $\log n$，所以，当分区大小比例是 $1:9$ 时，快速排序的时间复杂度仍然是 $O(n\log n)$。

   刚刚我们假设 $k=9$，那如果 $k=99$，也就是说，每次分区极其不平均，两个区间大小是 $1:99$，这个时候的时间复杂度是多少呢？

   我们可以类比上面 $k=9$ 的分析过程。当 $k=99$ 的时候，树的最短路径就是 $\log_{100}​ n$，最长路径是 $\log_{\frac{100}{99}} ​n$，所以总遍历数据个数介于 $n\log_{100} ​n$ 和 $n\log_{\frac{100}{99}​} ​n$ 之间。

   由上可知，当 $k$ 的值不确定时，总遍历数据个数介于 $n\log_{1+k} ​n$ 和 $n\log_{\frac{1+k}{k}​} ​n$ 之间。

   尽管底数变了，但是时间复杂度也仍然是 $O(n\log n)$。也就是说，对于 $k$ 等于 $9，99$， 甚至是 $999，9999……$，只要 $k$ 的值不随 $n$ 变化，是一个事先确定的常量，那快排的时间复杂度就是 $O(n\log n)$。所以，从概率论的角度来说，快排的平均时间复杂度就是 $O(n\log n)$。

扩展

思考题：如何利用快排找到数组第k大的元素

为了便于找出数组 索引(index) 与 k 之间的关系，我画了一张表格，该表格的基础是数组按从小到大排列，其中 len 表示数组的长度

const arr = [1, 2, 3, 4, 5]

第k大(k的取值如下)	对应的索引位(index)	备注
1	len - 1	第1大元素对应的索引位为len - 1
2	len - 2	第2大元素对应的索引位为len - 2
3	len - 3	第3大元素对应的索引位为len - 3
...	...	...
k	len - k	第k大元素对应的索引位为len - k

可知数组第 k 大的元素的索引为 len - k。根据这个结论找到数组第k大的元素就简单多了。具体规则如下：

1. 通过一次分区操作可得该次分区结果的索引，即 partition 函数的返回值 q
2. 比较 q 与 len - k 的大小
   1. q == len -k，说明数组第k大的元素就是索引为q的元素，找到了，返回结果
   2. q > len -k，说明数组第k大的元素在q的左边，所以对q的左半区间进行上述相同的分区操作
   3. q < len -k，说明数组第k大的元素在q的右边，所以对q的右半区间进行上述相同的分区操作

代码如下

/**
 * 找到数组第k大的元素
 * @param {*} arr 数组
 * @param {*} n 数组的空间大小
 * @param {*} k 第k大元素
 * @returns 
 */
function findKth(arr, n, k) {
  function _findKth(arr, l, r) {
    if (l > r) return -1;
    // 通过分区函数找到第 q 大的元素
    const q = partition(arr, l, r);
    if (q == (n - k)) {// 找到了直接返回
      return arr[q];
    } else if (q > (n - k)) {
      return _findKth(arr, l, q - 1)
    } else {
      return _findKth(arr, q + 1, r);
    }
  }
  return _findKth(arr, 0, n - 1);
}

参考资料

• 数据结构与算法之美·王争·极客时间 (opens new window)