堆排序
lkj 4/8/2022 排序
# 一、堆这种数据结构的两个特点
- 堆是一种完全二叉树
- 堆中的每个节点都大于等于它的左子节点和右子节点,此种堆也称为大顶堆,以下内容所说的堆没有特殊说明均指大顶堆
# 二、如何存储一个堆
通过指针(左右指针指向左右子节点)的形式,因为堆也是一种完全二叉树
通过数组的形式,因为堆是一种完全二叉树,而完全二叉树最主要的特点就是可以通过数组下标的关系找到其父子节点位置。比如下标为
i的节点,其左子节点下标为i * 2,右子节点下标为i * 2 + 1,父节点下标为i/2,我画了一个用数组存储堆的例子,如下图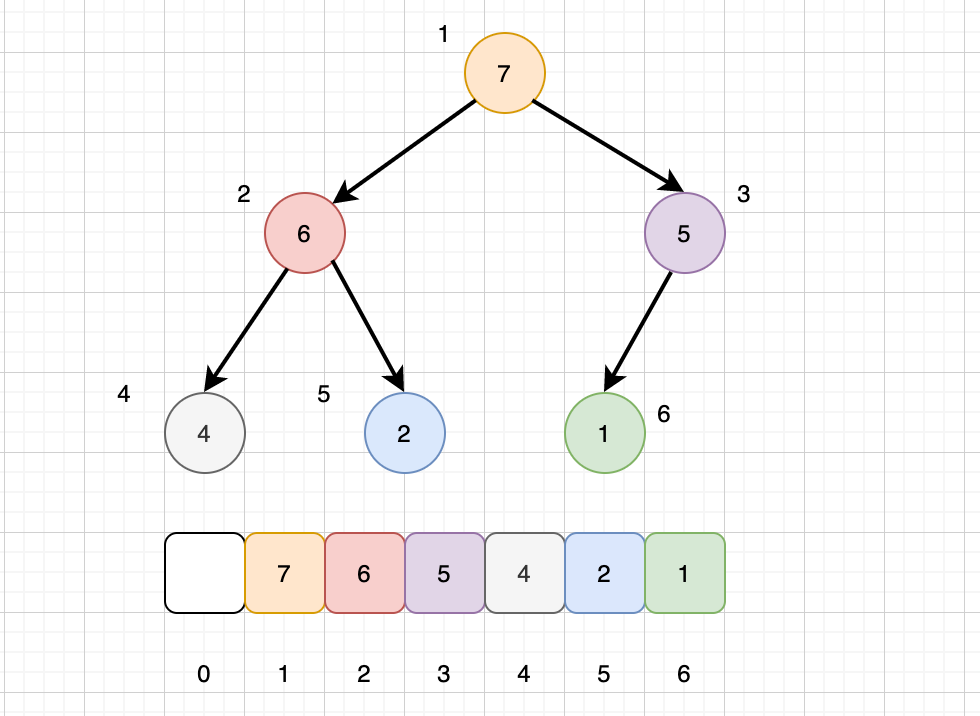
# 三、堆的操作
插入,插入一个节点数据后如何保证堆的有序?
将插入的节点放到堆的末尾,然后让新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系,我们就互换两个节点。一直重复这个过程,直到父子节点之间满足刚说的那种大小关系。
此种堆的有序化我们称之为由下而上的堆有序化,也称为上浮(swim)操作
删除,删除一个数据后如何保证堆的有序?
删除的是堆顶节点,我们把最后一个节点放到堆顶,然后利用同样的父子节点对比方法来堆顶元素进行堆有序化。对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止。
此种堆的有序化我们称之为由上而下的堆有序化,也称为下沉(sink)操作
「代码如下」
/**
* 利用数组实现的堆
* @param {*} capacity 堆可以存储的最大数据量
*/
function Heap(capacity) {
this.arr = new Array(capacity + 1).fill(-1);
this.n = capacity;
this.count = 0; // 堆中已经存储的数据个数
}
// 插入元素,并维持堆的有序(自下往上,上浮)
Heap.prototype.insert = function (data) {
if (this.count == this.n) return false; // 堆满了,直接退出
this.arr[++this.count] = data;
// 堆的有序化,上浮操作
swim(this.arr, this.count)
return true;
}
// 删除堆顶元素,并维持堆的有序(自上往下,下沉)
Heap.prototype.deleteMax = function () {
if (this.count == 0) return false; // 堆中没有元素,直接结束
swap(this.arr, 1, this.count--); // 交换堆顶元素与堆中的最后一个元素,同时令堆中的数据个数减1
// 开始堆的有序化,下沉操作
sink(this.arr, 1, this.count);
return true;
}
/**
* 堆的有序化,上浮操作
* @param {*} arr 数组
* @param {*} i 上浮的节点索引
*/
function swim(arr, i) {
while (true) {
// 获取当前进行堆有序化节点的父节点索引
let parent = Math.floor(i / 2);
if (parent > 0 && arr[i] > arr[parent]) {
// 如果有父节点并且比父节点的值要大,则交换
swap(arr, i, parent);
// 更新当前要进行堆有序化的节点索引
i = parent;
} else {
break;
}
}
}
/**
* 堆的有序化,下沉操作
* @param {*} arr 数组
* @param {*} i 要下沉的节点索引
* @param {*} n 数组中的数据个数
*/
function sink(arr, i, n) {
while (true) {
let maxPos = i; // 记录较大值的节点索引
// 下述两个if操作的目的是找到`当前节点`、`左子节点`、`右子节点`中最大的节点并将其索引值赋给maxPos
// 如果有左子节点,并且当前节点值比左子节点的值小,则更新较大值的节点索引为左子节点的索引
if (i * 2 <= n && arr[i] < arr[i * 2]) maxPos = i * 2;
// 如果有右子节点,并较大值的节点比右子节点的值小,则更新较大值的节点索引为右子节点的索引
if (i * 2 + 1 <= n && arr[maxPos] < arr[i * 2 + 1]) maxPos = i * 2 + 1;
// 如果较大值的节点就是当前要处理的节点,直接结束
if (maxPos == i) break;
// 否则交换
swap(arr, i, maxPos);
// 更新进行堆有序化的节点索引
i = maxPos;
}
}
// 交换数组指定位置的两个元素
function swap(arr, i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
const heap = new Heap(6)
heap.insert(1)
heap.insert(2)
heap.insert(3)
heap.insert(4)
heap.insert(5)
heap.insert(6)
console.log(heap.arr)// [0, 6, 4, 5, 1, 3, 2]
heap.deleteMax()
heap.deleteMax()
heap.deleteMax()
heap.deleteMax()
heap.deleteMax()
heap.deleteMax()
console.log(heap.arr)// [0, 1, 2, 3, 4, 5, 6]
# 四、建堆
如何将一个随机打乱的数组建成一个堆?
假定随机打乱的数组是一个堆(实际不是),然后对堆中的所有非叶子节点进行下沉(sink)操作,即可建成一个堆。而叶子节点往下堆化(下沉操作)其实是跟自己比较,没有意义,所以我们只对堆中的所有非叶子节点进行下沉(sink)操作即可。
「代码如下」
/**
* 根据传入的随机数组构建一个堆
* @param {*} arr 数组
* @param {*} n 数组元素个数
*/
function buildHeap(arr, n) {
const noLeafNodeIndex = Math.floor(n / 2);
for (let i = noLeafNodeIndex; i > 0; i--) {
sink(arr, i, n)
}
}
// 数组的第一个(下标为0)元素是用来占位的,不存储任何数据
const arr = [-1, 1, 2, 3, 4, 5, 6]
buildHeap(arr, 6)
console.log(arr) // [-1, 6, 5, 3, 4, 2, 1]
# 五、堆排序
如何利用建好的堆进行数组的排序? 比如堆中有n个数据,
- 将堆顶元素与堆尾元素进行交换,然后对堆顶元素在区间[1, n-1]中进行下沉操作,使得满足堆的特性
- 重复 1 的操作,不断减少区间至[1, 1],即剩下一个元素时停止,此时完成堆排序
/**
* 堆排序
* @param {*} arr 随机打乱的数组
* @param {*} n 数组中元素个数
*/
function heapSort(arr, n){
buildHeap(arr, n) // 先构建一个堆
while(n > 1){// 不断删除堆顶元素
// 交换堆顶元素与堆尾元素,同时令堆元素个数减1
swap(arr, 1, n--);
// 开始堆的有序化,即下沉操作
sink(arr, 1, n)
}
}
// 数组的第一个(下标为0)元素是用来占位的,不存储任何数据,默认为-1
const arr = [-1, 3, 1, 4, 2, 6, 5]
heapSort(arr, 6)
console.log(arr) // [-1, 1, 2, 3, 4, 5, 6]
# 参考资料
- 书籍:算法(第4版) p195~p208
- 数据结构与算法之美·王争·极客时间 (opens new window)
