栈的应用

lkj 4/8/2022 栈

# 一、栈的基本实现

栈这种数据结构即可以通过数组实现，也可以通过链表实现

用数组实现的栈，我们叫作顺序栈
用链表实现的栈，我们叫作链式栈

/**
 * 顺序栈：通过数组实现栈数据结构
 * @param {*} n 栈的空间大小
 */
function ArrayStack(n) {
  this.arr = new Array(n).fill(0);
  this.n = n; // 栈的空间大小
  this.count = 0; //栈顶指针
}
// 入栈
ArrayStack.prototype.push = function (value) {
  if (this.count >= this.n) return false;
  this.arr[this.count++] = value;
  return true;
}
// 出栈
ArrayStack.prototype.pop = function () {
  // 如果栈为空，直接返回false
  if (this.count === 0) return false;
  return this.arr[--this.count];
}
// 获取栈顶元素
ArrayStack.prototype.pick = function () {
  if (this.count === 0) return false;
  return this.arr[this.count-1];
}

# 二、表达式求值

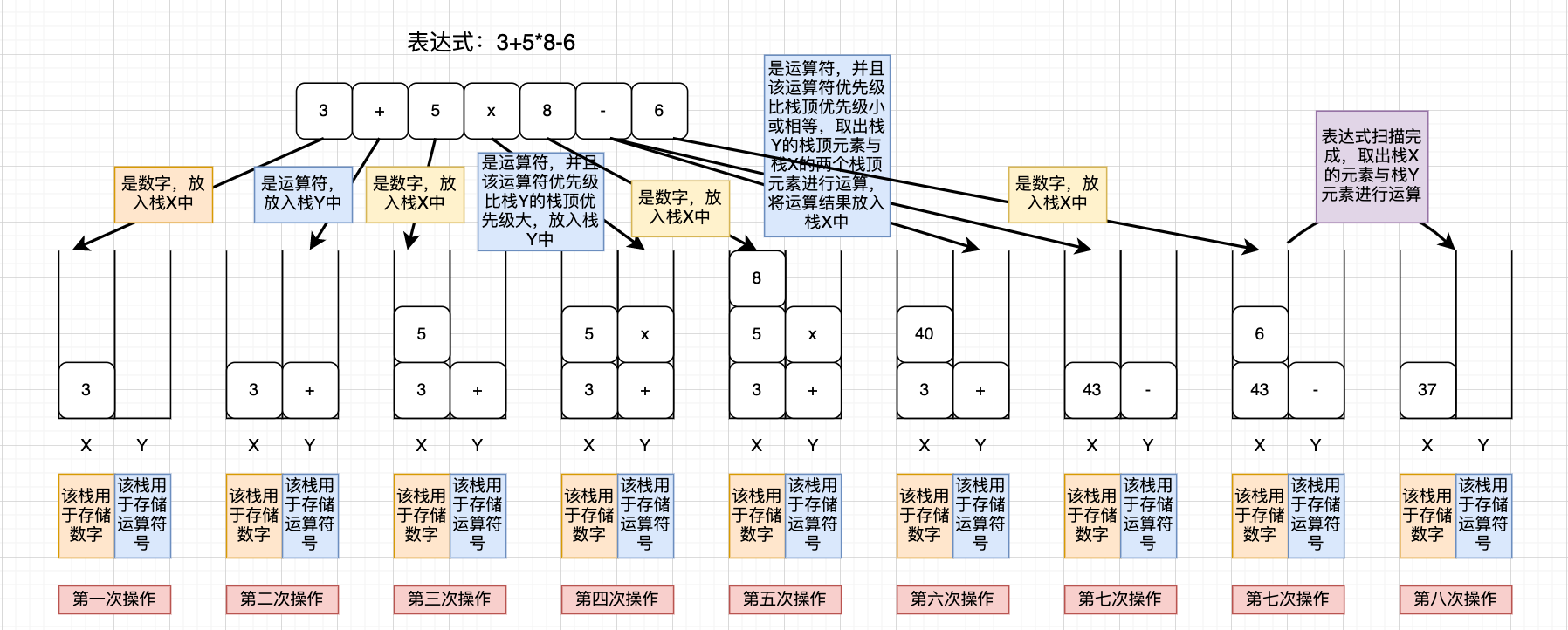
为了方便解释，我将算术表达式简化为只包含加减乘除四则运算，比如：34+13*9+44-12/3。对于这个四则运算，我们人脑可以很快求解出答案，但是对于计算机来说，理解这个表达式本身就是个挺难的事儿。如果换作你，让你来实现这样一个表达式求值的功能，你会怎么做呢？
实际上，编译器就是通过两个栈来实现的。其中一个是保存操作数的栈，另一个是保存运算符的栈。我们从左向右遍历表达式，当遇到数字，我们就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较
如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较

以 3+5*8-6 为例

代码

// const expression = "34+13*9+44-12/3";
const stackX = new ArrayStack(10); //用于存储数字的栈
const stackY = new ArrayStack(10); //用于存储运算符的栈

function getOperationRes(expression) {
  let len = expression.length;
  for (let i = 0; i < len; i++) {
    const number = expression[i];
    if (+number) { // 是数字，压入栈X中
      stackX.push(+number)
    } else { // 是运算符
      if (stackY.count > 0) { // 栈stackY不为空
        const top = stackY.pick(); // 取出stackY的栈顶元素进行比较
        // 比较此刻扫描到的元素与栈顶元素优先级
        const res = compPriority(expression[i], top)
        if (res) { // 此刻扫描到的元素比栈顶元素优先级高，将扫描到的元素（运算符）压入栈Y中
          stackY.push(expression[i])
        } else { // 此刻扫描到的元素比栈顶元素优先级低或等于，调用compute进行运算
          compute(stackX, stackY)
          i--;
        }
      } else { // 栈stackY为空，直接入栈
        stackY.push(expression[i])
      }
    }
  }
  // 计算表达式扫描完成后的处理逻辑
  if (stackY.count > 0) { // 用于存储运算符的栈stackY中有元素，则进行计算
    while (stackY.count > 0) {
      compute(stackX, stackY)
    }
    // 计算完成后返回tackX中的栈顶元素
    return stackX.pick();
  } else {// 用于存储运算符的栈stackY中无元素，直接返回stackX中的栈顶元素
    return stackX.pick();
  }
}

/**
 * 比较两个运算符的优先级
 * @param {*} operation1 
 * @param {*} operation1 
 */
function compPriority(operation1, operation2) {
  const operations = {
    "+": 1,
    "-": 1,
    "*": 2,
    "/": 2,
  }
  return operations[operation1] > operations[operation2] ? true : false
}

/**
 * 取出栈stackX中的栈顶两个数字和stackY中的栈顶运算符进行运算得出结果，将结果压入栈stackX中
 * @param {*} stackX 
 * @param {*} stackY 
 */
function compute(stackX, stackY) {
  const topOperation = stackY.pop();
  const rightNumber = stackX.pop();
  const leftNumber = stackX.pop();
  if (topOperation === "+") {
    stackX.push(leftNumber + rightNumber)
  } else if (topOperation === "-") {
    stackX.push(leftNumber - rightNumber)
  } else if (topOperation === "*") {
    stackX.push(leftNumber * rightNumber)
  } else {
    stackX.push(leftNumber / rightNumber)
  }
}

const res = getOperationRes(["3", "+", "13", "*", "9", "+", "44", "-", "12", "/", "3"])
console.log(res)

# 三、括号匹配

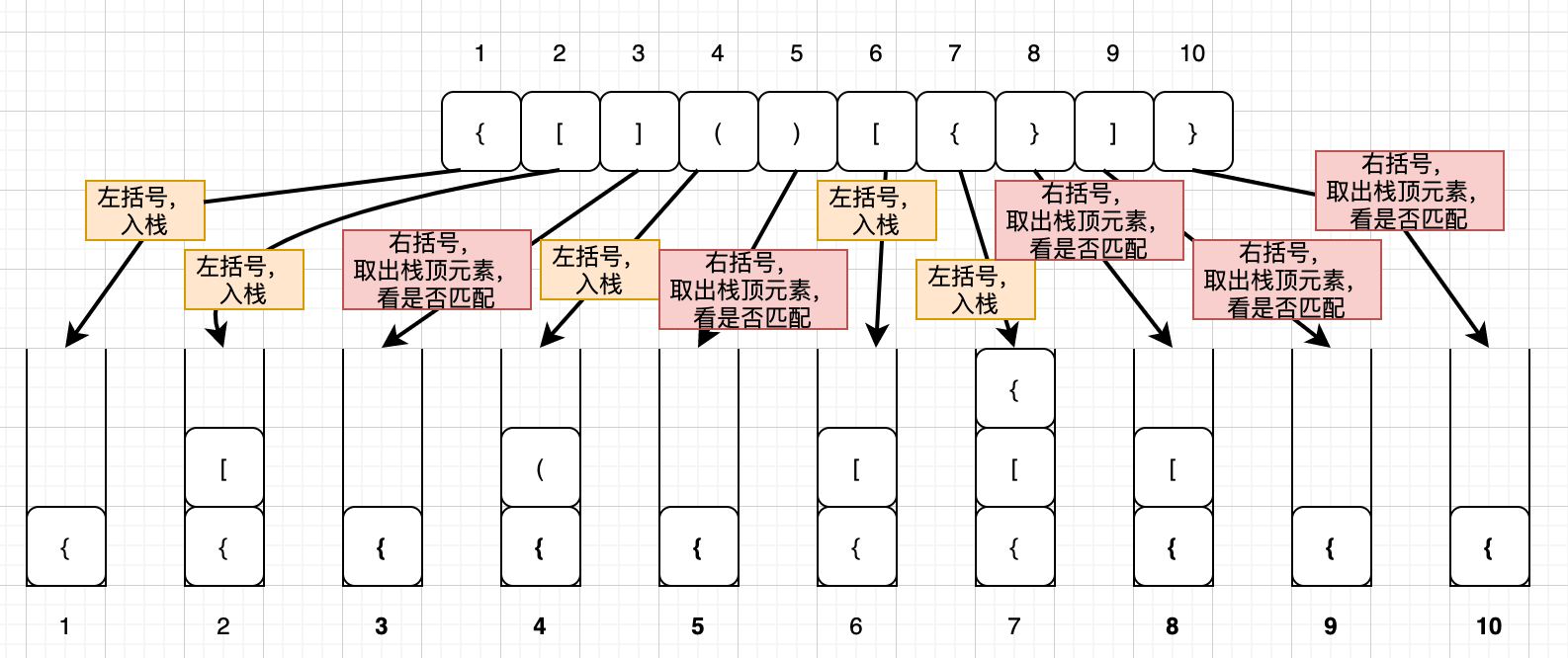
说明：表达式中只包含三种括号，圆括号 ()、方括号[]和花括号{}，并且它们可以任意嵌套。比如，{[] ()[{}]} 或 [{()}([])] 等都为合法格式，而 {[}()] 或 [({)] 为不合法的格式
那我现在给你一个包含三种括号的表达式字符串，如何检查它是否合法呢？
规则：我们用栈来保存未匹配的左括号，从左到右依次扫描字符串。
1. 当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。
2. 如果能够匹配，比如 “(” 跟 “)” 匹配，“[” 跟 “]” 匹配，“{” 跟 “}” 匹配，则继续扫描剩下的字符串
3. 如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。
4. 当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式；否则，说明有未匹配的左括号，为非法格式。

代码

/**
 * 判断一个括号字符串是否合法
 * @param {*} str 括号字符串
 * @returns 
 */
function isLegal(str) {
  let len = str.length;
  for (let i = 0; i < len; i++) {
    const bracket = str[i];
    const isLeftBracket = leftOrRight(bracket)
    if (isLeftBracket) { // 是左括号, 入栈
      stack.push(bracket)
    } else { // 是右括号，取出栈顶元素，判断是否匹配
      const ele = stack.pop();
      if (isMatch(ele, bracket)) { // 匹配，进入下一次循环
        continue;
      } else {
        return false;
      }
    }
  }
  // 所有的括号都扫描完成之后的处理逻辑
  if (stack.count === 0) {// 栈为空，说明字符串为合法格式
    return true;
  } else {// 栈不为空，说明有未匹配的左括号，为非法格式
    return false;
  }
}

/**
 * 判断左右括号是否匹配
 * @param {*} left 左括号
 * @param {*} right 右括号
 * @returns 
 */
function isMatch(left, right) {
  const brackets = {
    "(": ")",
    "[": "]",
    "{": "}"
  }
  return (brackets[left] == right) ? true : false;
}

/**
 * 判断传入的括号是左括号还是右括号
 * 若是左括号，返回true
 * 若是右括号，返回false
 * @param {*} bracket 
 * @returns  
 */
function leftOrRight(bracket) {
  const leftBrackets = ["(", "[", "{"];
  return leftBrackets.includes(bracket) ? true : false;
}

const stack = new ArrayStack(10)
const str = "{[()]";
const res = isLegal(str)
console.log(res)

# 参考资料

数据结构与算法之美·王争·极客时间 (opens new window)

栈与队列的介绍用栈实现队列

LKJ's blog

Choose mode

栈的应用

栈的应用

# 一、栈的基本实现

# 二、表达式求值

# 三、括号匹配

# 参考资料