环形链表II

题目 LeetCode (opens new window)

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

示例：

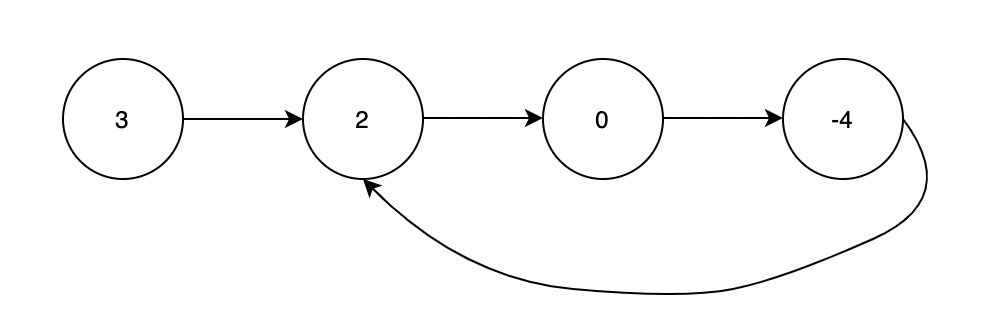
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

思路

由上篇文章 环形链表 可知环形链表的相遇点，此时在相遇处令快指针（或慢指针）指向链表的起始节点（头节点），然后令快、慢指针以相同步伐继续走，则快、慢指针再次相遇处即为环的起点。

提问：为什么上述思路就是正确的呢？🤔

$$证明如下 \Downarrow$$

---

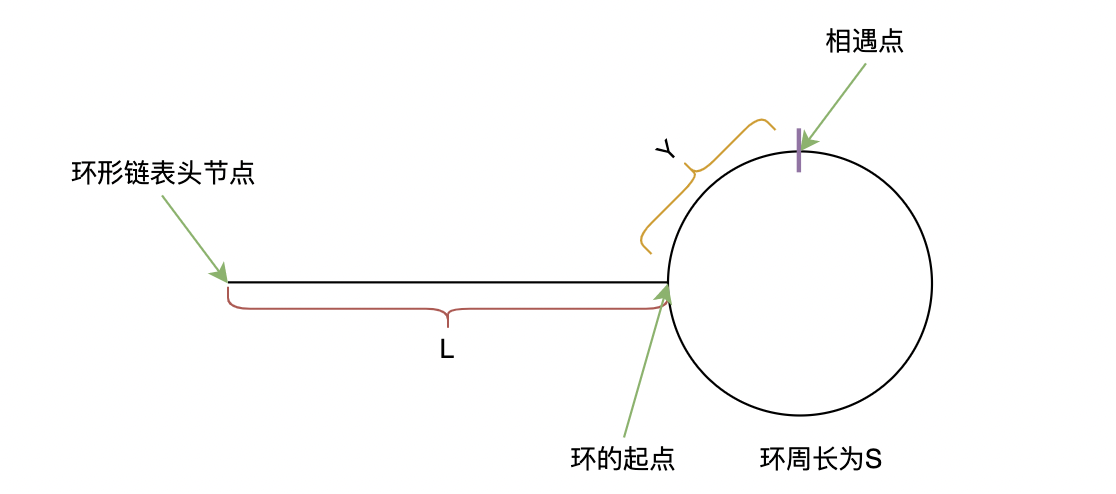
快、慢指针从环形链表头节点开始，令快指针每秒走 $2$ 步，慢指针每秒走 $1$ 步，快、慢指针走到相遇处时花了 $x$ 秒。

那么在相遇处时快指针共走了 $2x$ 步，慢指针共走了 $x$ 步。假设快指针走的环的圈数为 $m$ 圈，慢指针走的环的圈数为 $n$ 圈。那么此时，对于快指针就有如下等式

$$2x=m*S+Y+L \text{ (1)}$$

对于慢指针就有如下等式

$$x=n*S+Y+L \text{ (2)}$$

令 $(2)*2-(1)$ 可得 $0=(2n-m)*S+Y+L$ ，即 $L=(m-2n)*S-Y$。由于 $L\geqslant 0$ ，所以 $m-2n$ 的值应为 $\geqslant 1$ 的整数，那么可得 $L=(m-2n-1)*S+S-Y$。不妨令 $p=m-2n-1$，此时 $L=p*S+S-Y$，其中 $p\geqslant 0$。

由于在相遇时令快指针指向环形链表的头节点，然后快、慢指针以相同步伐继续走。当快指针走到环的起点时，也就走了 $L$ 步，又因为 $L=p*S+S-Y$，所以快指针走了 $p*S+S-Y$ 步。由于快、慢指针是以相同步伐走的，也就是说慢指针从相遇处开始走也走了 $p*S+S-Y$ 步，所以此时我只要证明慢指针从相遇处开始走的 $p*S+S-Y$ 步后恰好停在环的起点即可。而从相遇点以顺时针方向到环的起点距离恰好为 $S-Y$ 步，那么慢指针走的 $p*S+S-Y$ 步用文字描述的话就可以是：慢指针先走了 $S-Y$ 步到环的起点，再在环的起点沿顺时针方向又走了 $p$ 圈，最终还是回到环的起点与快指针相遇。

---

$$证明 \quad 毕 \Uparrow$$

代码

// 若一个链表成环，返回环的起始节点
function detectCycle(head) {
  // 初始化快、慢指针指向头节点
  let slow = head;
  let fast = head;
  while (fast !== null && fast.next !== null) {
    // 慢指针每次前进一步
    slow = slow.next;
    // 快指针每次前进两步
    fast = fast.next.next;
    // 如果存在环，快慢指针必然相遇，退出当前while循环
    if (slow === fast) break;
  }

  // 无环，则返回null
  if(fast == null || fast.next == null) return null;

  // 让慢指针重新指向头节点
  slow = head;
  while(slow!==fast){
    // 让快慢指针以相同步伐前进
    slow = slow.next;
    fast = fast.next;
    // 快慢指针相遇的点即为环的起始节点
    if(slow === fast) return slow;
  }
  return slow;
}

参考资料

• 前端算法系统练习: 链表篇完结 (opens new window)