最长回文子序列

题目 LeetCode (opens new window)

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例 2：

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

思路

1. 明确 dp 数组以及下标的含义

$dp[i][j]$ 表示字符串 $s$ 在索引 $i～j$ 范围内的最长回文子序列长度为 $dp[i][j]$

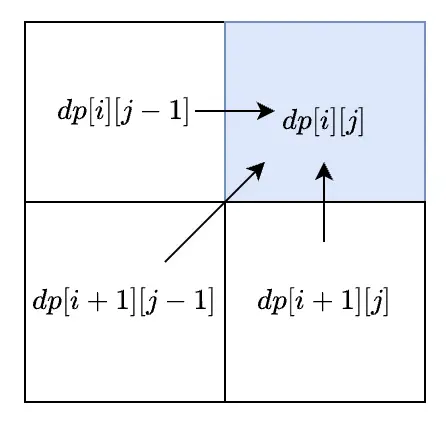
2. 确定状态转移方程

即能否通过 $dp[i+1][j-1]$（之前的状态） 推导出 $dp[i][j]$（现在的状态） 呢？是可以的

如果 $s[i] == s[j]$ 则 $dp[i][j] = dp[i+1][j-1] + 2$

如果 $s[i] != s[j]$ 则 $dp[i][j] = max(dp[i+1][j], dp[i][j-1])$

通过下图辅助理解

3. 确定 dp 数组的初始状态

如果 $i == j$ 说明只有一个字符，则 $dp[i][j] = 1$

如果 $i > j$ 这种情况是不可能的，则 $dp[i][j] = 0$

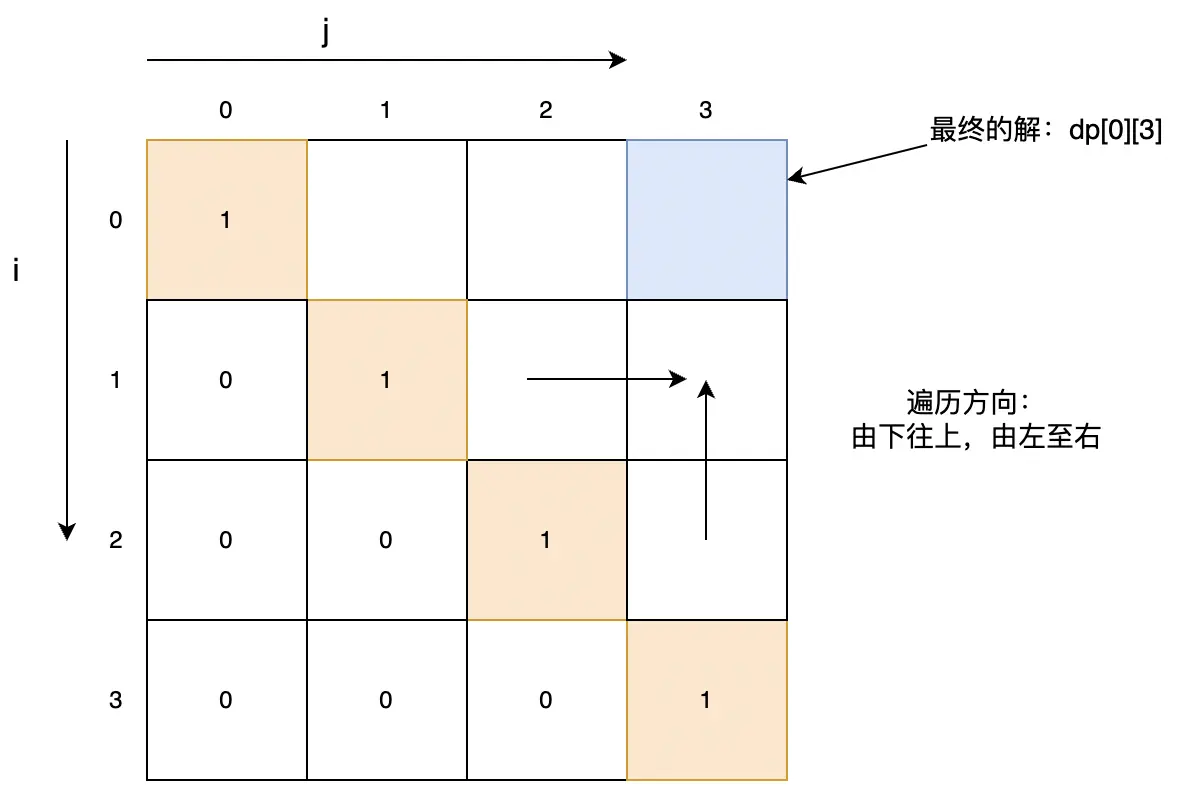
4. 确定 dp 数组的遍历顺序

通过分析可知 $dp$ 数组的遍历顺序为由下到上、由左至右

5. 返回最终的解

即返回 $dp[0][len-1]$，其中 $len$ 为字符串的长度

代码

/**
 * @param {string} s
 * @return {number}
 */
var longestPalindromeSubseq = function (s) {
    let len = s.length;
    let dp = new Array(len)
    for (let i = 0; i < len; i++) {
        dp[i] = new Array(len).fill(0)
    }
    for (let i = 0; i < len; i++) { // dp 数组的初始化
        dp[i][i] = 1;
    }
    for (let i = len - 2; i >= 0; i--) {
        for (let j = i + 1; j < len; j++) {
            if (s[i] == s[j]) {
                dp[i][j] = dp[i + 1][j - 1] + 2;
            } else {
                dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
            }
        }
    }
    // 返回最终的解：dp[0][len-1]
    return dp[0][len - 1];
};

空间优化

由以上分析可知 $dp[i][j]$ 只取决于 $dp[i+1][j-1]、dp[i][j-1]、dp[i+1][j]$ 这三个状态，完全没有必要定义二维 $dp$ 数组。那能否将二维 $dp$ 数组转化为一维 $dp$ 数组来以进行空间优化呢？是可以的

参考资料

• labuladong的算法小抄 (opens new window)
• 代码随想录 (opens new window)